Question

A student believes that less than 50% of students at his college receive financial aid. A random sample of 120 students was taken. Sixty-five percent of the students in the sample receive financial aid. Test the hypothesis at the 2% level of significance. What are the p-value and conclusion?

Answer 1

p= 0.9995 and we can conclude that students receiving aid is more than 50% according to the sample results in 2% significance level.

Explanation:

`H_(0)`: less than or equal 50% of students at his college receive financial aid

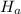`H_(a)`: more than 50% of students receive financial aid.

According to the nul hypothesis we assume a normal distribution with proportion 50%.

z-score of sample proportion can be calculated using the formula:

z=
`(X-M)/((s)/(√(N) ) )` where

• X is the sample proportion (0.65)
• M is the null hypothesis proportion (0.5)
• s is the standard deviation of the sample (
  `√(0.5*(1-0.5))`)
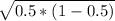• N is the sample size (120)

then z=
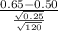`(0.65-0.50)/((√(0.25))/(√(120) ) )` ≈ 3,29

thus p= 0.9995 and since p<0.02 (2%), we reject the null hypothesis.