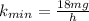Question

A person of mass m will bungee-jump from a bridge over a river where the height from the bridge to the river is h. The bungee cord has an un-stretched length of 23h and when it stretches beyond its equilibrium length it behaves as a spring with spring constant k. Find an expression for the minimum spring constant k that will stop the person just before hitting the river (ignore the height of the person), in terms of m, g, and h.

Answer 1

Answer:
`k_(min)=(18mg)/(h)`

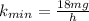
Step-by-step explanation:

Given

mass of person is m

Distance between bridge and river is h

chord has an un-stretched length of
`(2h)/(3)`

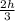
Let spring constant be k

Person will just stop before hitting the river

Conserve energy i.e. Potential Energy of Person is converted in to elastic energy of chord

`mgh=(kx^2)/(2)`

`x=h-(2h)/(3)=(h)/(3)`

`mgh=(kh^2)/(18)`

`k=(18mg)/(h)`

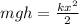
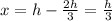
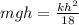
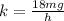
Thus
`k_(min)=(18mg)/(h)`