Answer:
Explanation:
Given that the lengths of pregnancies in a small rural village are normally distributed with a mean of 267 days and a standard deviation of 17 days.
X is N(267,17) where x = length of pregnancies in days
For middle 50% we must have on either side 25% area
Hence z= ±0.675
Corresponding x score would be

---
Sample size = n =36
Std error of sample =

50% would be within
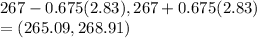
=between 265.1 and 268.9