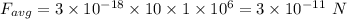Question

A spaceship of frontal area 10 m2 moves through a large dust cloud with a speed of 1 x 106 m/s. The mass density of the dust is 3 x 10-18 kg/m3. If all the particles of dust that impact the spaceship stick to it, find the average decelerating force that the impacting particles exert on the ship. (You may assume that the mass of dust which sticks to the spacecraft is negligible compared to the mass of the spacecraft.)

Answer 1

The decelerating force is
`3* 10^(- 11)\ N`

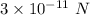
Solution:

As per the question:

Frontal Area, A =
`10\ m^(2)`

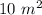
Speed of the spaceship, v =
`1* 10^(6)\ m/s`

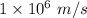
Mass density of dust,
`\rho_(d) = 3* 10^(- 18)\ kg/m^(3)`

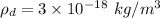
Now, to calculate the average decelerating force exerted by the particle:

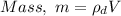`Mass,\ m = \rho_(d)V` (1)

Volume,
`V = A* v* t`

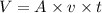
Thus substituting the value of volume, V in eqn (1):

`m = \rho_(d)(Avt)`

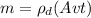
where

A = Area

v = velocity

t = time

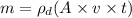`m = \rho_(d)(A* v* t)` (2)

`Momentum,\ p = \rho_(d)(Avt)v = \rho_(d)Av^(2)t`

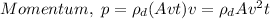
From Newton's second law of motion:

`F = (dp)/(dt)`

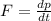
Thus differentiating w.r.t time 't':

`F_(avg) = (d)/(dt)(\rho_(d)Av^(2)t) = \rho_(d)Av^(2)`

where

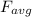`F_(avg)` = average decelerating force of the particle

Now, substituting suitable values in the above eqn:

`F_(avg) = 3* 10^(- 18)* 10* 1* 10^(6) = 3* 10^(- 11)\ N`