Question

An inverted pyramid is being filled with water at a constant rate of 70 cubic centimeters per second. The pyramid, at the top, has the shape of a square with sides of length 7 cm, and the height is 10 cm. Find the rate at which the water level is rising when the water level is 4 cm.

Answer 1

Rate of change in height of the water level is 2.91 cm per second.

Explanation:

Height of the inverted pyramid = 10 cm

Length of the square base = 7 cm

If water is filled up to the level of h cm then the volume of water up to height h will be

V =
`(1)/(3)(\text {Area of the base})* (h)`

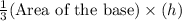
V =
`(1)/(3)(x^(2) )* (h)`

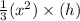
It is given that rate of water is filling with 70 cubic centimeters per second.

`(dV)/(dt)=70`

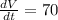
From two similar triangles in the figure attached,

`(x)/(h)=(7)/(10)`

`x=(7h)/(10)`

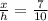
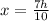
By replacing the value of h,

V =
`(1)/(3)((7h)/(10))^(2)h`

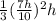
V =
`(1)/(3)((49h^(2) )/(100))h`

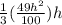
V =
`(1)/(3)((49h^(3))/(100))`

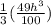
Now we integrate the equation with respect to time 't'

`(dV)/(dt)=(d)/(dt)((1)/(3)* (49h^(3) )/(100))`

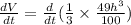
70 =
`(49h^(2) )/(100)* (dh)/(dt)`

`(dh)/(dt)=(100* 70)/(49h^(2))`

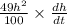
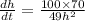
For h = 7 cm

`(dh)/(dt)=(70* 100)/(49* 49)`

`(dh)/(dt)=2.91`

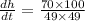
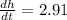
Therefore, rate of change in height of the water level is 2.91 cm per second.