Answer:
Rate of change in height of the water level is 2.91 cm per second.
Explanation:
Height of the inverted pyramid = 10 cm
Length of the square base = 7 cm
If water is filled up to the level of h cm then the volume of water up to height h will be
V =

V =
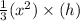
It is given that rate of water is filling with 70 cubic centimeters per second.
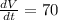
From two similar triangles in the figure attached,
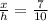
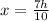
By replacing the value of h,
V =
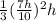
V =
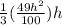
V =

Now we integrate the equation with respect to time 't'
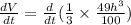
70 =
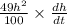
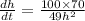
For h = 7 cm
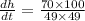
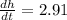
Therefore, rate of change in height of the water level is 2.91 cm per second.