Question

Aerotron Electronics is considering the purchase of a water filtration system to assist in circuit board manufacturing. The system costs $70,000. It has an expected life of 7 years at which time its salvage value will be $7,500. Operating and maintenance expenses are estimated to be $7,000 per year. If the filtration system is not purchased, Aerotron Electronics will have to pay Bay City $44,000 per year for water purification. If the system is purchased, no water purification from Bay City will be needed. Aerotron Electronics must borrow 1/2 of the purchase price, but they cannot start repaying the loan for 2 years. The bank has agreed to 3 equal annual payments, with the 1st payment due at the end of year 2. The loan interest rate is 8% compounded annually. Aerotron Electronics, MARR is 10% compounded annually. Click here to access the TVM Factor Table Calculator What is the annual worth of this investment?$ Carry all interim calculations to 5 decimal places and then round your final answer to the nearest dollar. The tolerance is ±10. What is the decision rule for judging the attractiveness of investments based on annual worth? Should Aerotron Electronics buy the water filtration system?

Answer 1

Yes It will be accepted.

As the present worth (cost) of the water filtration

is far less than paying to Bay City for the purification

It decrease to $96,890.53‬ from $214,210.43 of the Bay Ciity Option

Step-by-step explanation:

Present worth if the system is not purchased:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C $ 44,000.00

time 7 years

rate 0.1

`44000 * (1-(1+0.1)^(-7) )/(0.1) = PV\\`

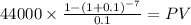
PV $214,210.4280

We will now compare the value of the water filtration system:

F0 investment: 70,000 / 2 = 35,000

loan payment:

principal after two-years grace period:

rate 0.08000

`35000 \: (1+ 0.08)^(2) = Amount`

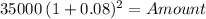
Amount 40,824.00

Then there is 3 payment annuity-due as it begins at the beginning right away after the grace period:

`PV / (1-(1+r)^(-time) )/(rate)(1+r) = C\\`

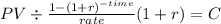
PV 40,824

time: 3 years

rate 0.08

`40824 / (1-(1+0.08)^(-3) )/(0.08)(1+.08) = C\\`

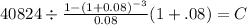
C $ 14,667.667

Present value of the annuity discounted at Minimim accepted rate of return of 10%:

`C * (1-(1+r)^(-time) )/(rate)(1+r) = PV\\`

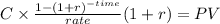
C 14,667.67

time years 3

rate 0.1

`14667.6668309512 * (1-(1+0.1)^(-3) )/(0.1)(1+0.10) = PV\\`

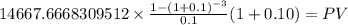
PV $40,123.9481

`(Maturity)/((1 + rate)^(time) ) = PV`

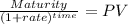
Maturity 40,123.95

time 2.00

rate 0.10000

`(40123.9481078087)/((1 + 0.1)^(2) ) = PV`

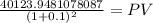
PV 33,160.29

present value of the maintenance expenses:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C $ 7,000.00

time 7 years

rate 0.1

`7000 * (1-(1+0.1)^(-7) )/(0.1) = PV\\`

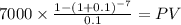
PV $34,078.9317

Present value of the salvage value:

`(Salvage)/((1 + rate)^(time) ) = PV`

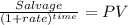
Salvage: $7,500.00

time 7 years

rate 0.10000

`(7500)/((1 + 0.1)^(7) ) = PV`

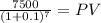
PV 3,848.69

Present worth of the water filtration system:

33,500 + +33,160.29 + 34,078.93 - 3,848.69 = 96,890.53‬