Answer:
The ecuation of the line is
y=-0.0068X+40
Explanation:
Hello!
To solve this question we must use the least-squares regression line equation, the equation is as follows
Y=mx+b
The values of m and b are found using the formulas in the attached image
To solve then we will use a table that to organize and extract all the values of the summations.
-Sum of X values
-Sum of Y values
- Sum of the product of X and Y
-
sum of x squared
-------X------------Y ---------(X)(Y)----------x^2
1)---- 2555------21,8 -----55699-----6528025
2)----2900------20,5----59450------8410000
3)----3330------19------- 63270-------11088900
4)---3725------14,2------52895------13875625
5)----4100-------11,6-------47560------16810000
------16610----- 87,1------278874-----56712550 SUMATORIES
Now we use the ecuation in atached image
remember that n= number of values =5
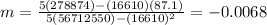
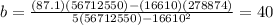
The ecuation of the line is
y=-0.0068X+40