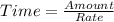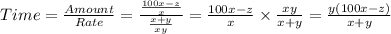Question

It takes machine A x hours to manufacture a deck of cards that machine B can manufacture in y hours. If machine A operates alone for z hours and is then joined by machine B until 100 decks are finished, for how long will the two machines operate simultaneously?

Answer 1

The expression that shows how long the two machines will operate simultaneously is:

`(y(100x-z))/(x+y)`

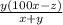
Explanation:

We know that:

x: hours to manufacture a deck of cards for machine A

y: hours to manufacture a deck of cards for machine B

z: hours that machine A operates alone

The number of decks manufactured only by machine A is:

`(z)/(x)`

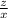
So, the remaining decks are given by:

`100-(z)/(x)=(100x-z)/(x)`

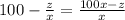
Then, the combined rate of machines A and B would be:

`(1)/(x) +(1)/(y) =(x+y)/(xy)`

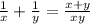
The work-rate formula is:

`Amount= Rate * Time`

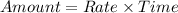
Hence, the time that the two machines work simultaneously is:

`Time=(Amount)/(Rate)`

`Time=(Amount)/(Rate) =((100x-z)/(x) )/((x+y)/(xy) ) ={(100x-z)/(x) * (xy)/(x+y)=(y(100x-z))/(x+y)`