Question

There are 435 representatives in the House. Suppose that 130 representatives are Democrats and 260 are Republicans; the rest are Independents. Assume that no representative belongs to more than one political party. A large infrastructure bill has barely been approved: 130 Democrats, 80 Republicans, and 10 Independents voted in favor of the bill. Given that a representative voted in favor of the bill, what is the probability that the representative is a Republican? Please enter an answer that is correct to four decimal places.

Answer 1

Given that a representative voted in favor of the bill, there is a 36.37% probability that he is a republican.

Explanation:

This can be formulated as the following problem:

What is the probability of B happening, knowing that A has happened.

It can be calculated by the following formula:

`P = (P(B).P(A/B))/(P(A))`

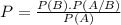
Where P(B) is the probability of B happening, P(A/B) is the probability of A happening knowing that B happened and P(A) is the probability of A happening.

In your problem we have that:

What is the probability that the representative is a Republican, given that he voted in favor of the bill?

P(B) is the probability that the representative is a Republican. There are 435 representatives in the house, of which 260 are republicans. So
`P(B) = (260)/(435) = 0.5977`

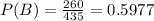
P(A/B) is the probability that the representative voted in favor of the bill, given that he is a Republican. There are 260 republicans, of which 80 voted in favor of the bill. So
`P(A/B) = (80)/(260) = 0.3077`

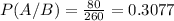
P(A) is the probability that someone voted in favor of the bill. There are 435 representatives, and 130 + 80 + 10 = 220 voted in favor of the bill. So
`P(A) = (220)/(435) = 0.5057`

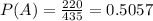
Applying to the formula

`P = (P(B).P(A/B))/(P(A)) = (0.5977*0.3077)/(0.5057) = 0.3637`

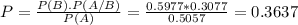
Given that a representative voted in favor of the bill, there is a 36.37% probability that he is a republican.