Question

The acceleration due to gravity on the moon is about one-sixth its value on earth. If a baseball reaches a height of 58 m when thrown upward by someone on the earth, what height would it reach when thrown in the same way on the surface of the moon?

Answer 1

It will reach 348 m.

Step-by-step explanation:

The gravity acceleration on Earth is

`g=9.81(m)/(s^(2))`

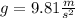
And for the Moon we write :

`g_(Moon)=(g)/(6)`

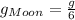
Being g the gravity acceleration on Earth

The speed equation on a vertical throw is the following :

`V_(f) ^(2)=V_(0) ^(2)-2g(y-y_(0))`

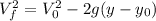
Where
`V_(f)` is the final speed of the throw

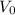`V_(0)` is the initial speed of the throw

g is the acceleration (generally the gravity acceleration)

y is the height reached

And
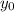`y_(0)` is the initial height

We define
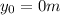`y_(0)=0m` putting the comparison plane on the Earth surface.

Applying the equation on Earth we have the following :

`0=V_(0) ^(2)-2g(58m)`

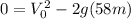
Because the final speed is 0 when the object is in it maximum height

and 58 m is the difference between the maximum height and
`y_(0)`

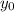
Then ⇒

`V_(0)^(2)=2g(58m)`

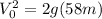
Finally,applying the equation on the Moon :

`0=V_(0)^(2)-2(g)/(6)(y-y_(0))`

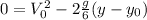
We use the expression of
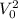`V_(0) ^(2)` that we calculated :

`0=2g(58m)-2(g)/(6)(y-y_(0))\\2(g)/(6)(y-y_(0))=2g(58m)`

`((y-y_(0)))/(6)=58m`

`y-y_(0)=348m`

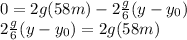
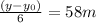
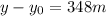
Then 348 m would be the height variation between
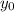`y_(0)` and y

If we define
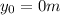`y_(0)=0m` putting the comparison plane on the Moon surface.

The height reached will be 348 m.