Question

A student failed to study for a multiple choice test. The test consists of ten questions with five choices for each answer. What is the probability that the student answers all questions incorrectly? What is the probability that the student will achieve at least 50% correct?

Answer 1

The probability that the student answers all questions incorrectly is 0.1074

The probability that the student will achieve at least 50% correct is 0.0328

Explanation:

This exercise adjust to a normal distribution, where:

p: probability that the student answers the question correctly (
`(1)/(5)`)

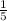n: number of questions (10 questions)

The binomial distribution is given by:

`P(X=x)=(n!)/(x!(n-x)!)* p^x * (1-p)^(n-x)`

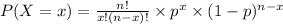
The probability that the student answers all questions incorrectly is P(X=0)

`P(X=0)=(10!)/(0!(10-0)!)* (0.2)^0 * (1-0.2)^(10-0)=0.1074`

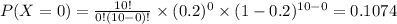
The probability that the student will achieve at least 50% correct is P(X≥5)

P(X≥5)= 1 - P(X=0) - P(X=1) - P(X=2) - P(X=3) - P(X=4)

P(X=0)=0.1074

`P(X=1)=(10!)/(1!(10-1)!)* (0.2)^1 * (1-0.2)^(10-1)=0.2684`

`P(X=2)=(10!)/(2!(10-2)!)* (0.2)^2 * (1-0.2)^(10-2)=0.3020`

`P(X=3)=(10!)/(3!(10-3)!)* (0.2)^3 * (1-0.2)^(10-3)=0.2013`

`P(X=4)=(10!)/(4!(10-4)!)* (0.2)^4 * (1-0.2)^(10-4)=0.0881`

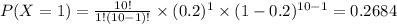
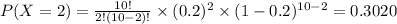
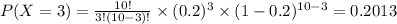
P(X≥5)= 1 - 0.1074 - 0.2684 - 0.3020 - 0.2013 - 0.0881=0.0328