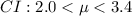Answer:
a)
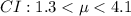
b)

c)
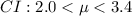
Explanation:
a) We have a sample of size n=10 and a sample mean of x=2.7.
The σ² of the population is known and is σ²=9 or σ=3.
For a CI of 85%, the z-value is 1.44.
Then the lower and upper limits of the CI are:
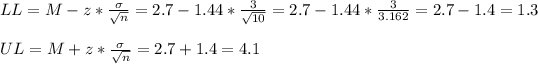
The 85% confidence interval for the mean is defined by the values LL=1.3 and UL=4.1.
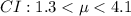
b) In this case, the variance of the population is unknown.
We have to estimate the variance of the population from the variance of the sample.
Sample data:
n = 100
x(mean) = 2.7
s² = 1.1
The CI is defined as
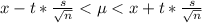
The value of t depends of the degrees of freedom and the percentage of confidence.
In this case, the degrees of freedom are n-1=100-1=99 and the CI is of 90%.
We look up in a t-table and the t-value for this conditions is 1.6604.
We can now calculate the CI
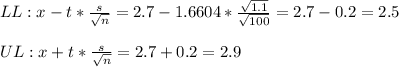
The 90% confidence interval for the mean is defined by the values LL=2.5 and UL=2.9.

c) In this case, the variance of the population is unknown.
We have to estimate the variance of the population from the variance of the sample.
Sample data:
n = 10
x(mean) = 2.7
s² = 1.1
The CI is defined as
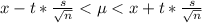
The value of t depends of the degrees of freedom and the percentage of confidence.
In this case, the degrees of freedom are n-1=10-1=9 and the CI is of 95%.
We look up in a t-table and the t-value for this conditions is 2.2622.
We can now calculate the CI
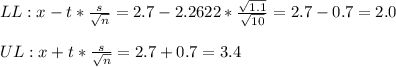
The 95% confidence interval for the mean is defined by the values LL=2.0 and UL=3.4.