Question

A drug company produces capsules that are designed to contain a specified amount of the active ingredient. The mean amount of the ingredient in one capsule is 150 mg, the SD is 5 mg and the distribution of the amount is Normal. A sample of 25 capsules is selected at random, and the production process is stopped if the average amount of the active ingredient in this sample is outside of the range [148 mg to 152 mg]. What is the probability (approximately) that the production is stopped

Answer 1

4.55%

Explanation:

Data provided in the question:

Given,

Number of samples of capsules, n = 25

mean amount of ingredient, μ = 150 mg

Standard deviation, σ = 5

Now,

`\bar{x}_1=148\ mg`

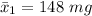
z-value will be

⇒ z₁ =
`\frac{\bar{x}_1-\mu}{((\sigma)/(\sqrt n))}`

or

⇒ z₁ =
`(148-150)/(((5)/(√(25))))`

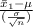
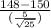
or

⇒ z₁ = - 2

similarly,

for
`\bar{x}_2=152\ mg`

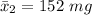
z-value will be

⇒ z₂ =
`\frac{\bar{x}_2-\mu}{((\sigma)/(\sqrt n))}`

or

⇒ z₂ =
`(152-150)/(((5)/(√(25))))`

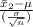
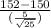
or

⇒ z₂ = 2

Now,

P( -2 < x < 2) = P( z < 2) - P(z < -2)

from the z-value vs P table, we have

= 0.9772498 - 0.0227501

= 0.9545

therefore,

Probability that the production is stopped = 1 - 0.9545

⇒ 0.0455 or

⇒ 0.0455 × 100%

= 4.55%