Answer:
The mean is
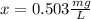
The 90% confidence interval is:
![i_(0.90)=[0.492(mg)/(L),0.514(mg)/(L)]](https://img.qammunity.org/2020/formulas/chemistry/college/iq4toeyca6ipzqtv6azqgtw2jswzgdro7h.png)
Step-by-step explanation:
1. First organize the data:
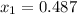

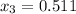
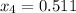
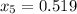
As there are 5 data, the sample size (n) is n=5
2. Calculate the mean x:
The mean is calculated adding up all the data and divide them between the sample size.
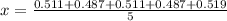
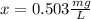
3. Find 90% confidence interval.
The formula to find the confidence interval is:
![i_(0.90)=[x+/-z_{(\alpha)/(2)}*((d)/(√(n)))]](https://img.qammunity.org/2020/formulas/chemistry/college/c2o5p944kul2ykp6rz74xt0rq9r8vbmydb.png) (Eq.1)
(Eq.1)
where x is the mean, d is the standard deviation and n is the sample size.
And
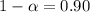
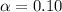
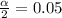
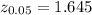
4. Find the standard deviation
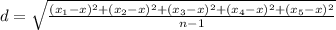

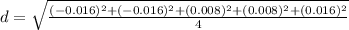
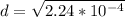

5. Replace values in (Eq.1):
![i_(0.90)=[0.503+/-1.645*((0.015)/(2.236))]](https://img.qammunity.org/2020/formulas/chemistry/college/3qo493sjsg0z3o9n2rcwmyuntj0bxb9psc.png)
For the addition:
![i_(0.90)=[0.503+1.645*((0.015)/(2.236))]](https://img.qammunity.org/2020/formulas/chemistry/college/2ortat07vsk723848ajmr2at0joh0kvtfs.png)
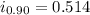
For the subtraction:
![i_(0.90)=[0.503-1.645*((0.015)/(2.236))]](https://img.qammunity.org/2020/formulas/chemistry/college/hwkmgrqtilnpirw15pf4t04smkz39k361p.png)

The 90% confidence interval is:
![i_(0.90)=[0.492,0.514]](https://img.qammunity.org/2020/formulas/chemistry/college/92drjb9rnc337gbkgbxkz5mezsgmelzvn9.png)