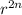Question

Give a recursive algorithm whose input is a real number r and a non-negative integer n, and whose output is r(2n) . Note that the exponent of r is 2n. Your algorithm should only use addition and multiplication operations and should not contain any loops.

Answer 1

Step-by-step explanation:

Let's use python for this:

recursive_exponent(n, r):

if n == 0:

return 1

else:

return r*recursive_exponent(n - 0.5, r)

To use this function, simply call it:

print(recursive_exponent(n, r))

The way it works is that n would start from top, and for each step it would get reduced by 0.5 until it gets to 0. Hence there will be 2n steps. At each step, r gets multiplied by itself. In the end r will multiplied by itself 2n times. Therefore,
`r^(2n)`