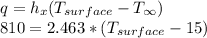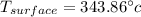Answer:
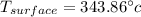
Step-by-step explanation:
We define the constant, so
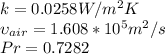
So, begin calculating the Reynolds number, so
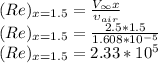
How reynolds number is greater than critical reynolds number, the flow
of the air is near about the turbulent flow,
we now calculate the local nusselt number

calculate the local convection heat transfer coefficient
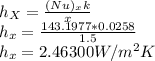
Apply the energy balance equation