Question

The area of a rectangular room is given by the trinomial x + 3x - 28. What are the possible

dimensions of the rectangle? Use factoring,
(x-7) and (x+4)
(x-7) and (x-4)
(x+7) and (x+4)
(x+7) and (x-4)

Answer 1

The possible dimensions of the rectangle are (x+7) and (x -4).

Explanation:

Here, the given expression for area of the rectangle is:
`x^(2)  + 3x - 28`

Now, Area of the rectangle = Length x Width

Hence, to find the dimensions, we need to factorize the given trinomial.

So,
`x^(2)  + 3x - 28 = x^(2)  + 7x - 4x- 28`

⇒
`x^(2)  + 7x - 4x- 28 = x(x+7)-4(x+7) = (x+7)(x-4)`

⇒
`x^(2)  + 3x - 28  = (x+7)(x-4)`

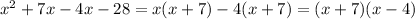
So, the factors of the polynomial are (x+7) and (x -4)

Hence, the possible dimensions of the rectangle are (x+7) and (x -4).