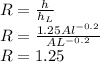Question

In an experiment, the local heat transfer over a flat plate were correlated in the form of local Nusselt number as expressed by the correlation Nux=0.035Re0.8xPr1/3 Determine the ratio of the average convection heat transfer coefficient (h) over the entire plate length to the local convection heat transfer coefficient (hx) (h/hx = L) at x = L.

Answer 1

R= 1.25

Step-by-step explanation:

As given the local heat transfer,

`Nu_x = 0.035 Re^(0.8)_x Pr^(1/3)`

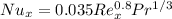
But we know as well that,

`Nu=(hx)/(k)\\h=(Nuk)/(x)`

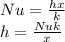
Replacing the values

`h_x=Nu_x (k)/(x)\\h_x= 0.035Re^(0.8)_xPr^(1/3) (k)/(x)`

Reynolds number is define as,

`Re_x = (Vx)/(\upsilon)`

Where V is the velocity of the fluid and \upsilon is the Kinematic viscosity

Then replacing we have

`h_x=0.035((Vx)/(\upsilon))^(0.8)Pr^(1/3)kx^(-1)`

`h_x=0.035((V)/(\upsilon))^(0.8)Pr^(1/3)kx^(0.8-1)`

`h_x=Ax^(-0.2)`

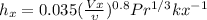
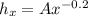
*Note that A is just a 'summary' of all of that constat there.

That is
`A=0.035((V)/(\upsilon))^(0.8)Pr^(1/3)k`

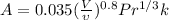
Therefore at x=L the local convection heat transfer coefficient is

`h_(x=L)=AL^(-0.2)`

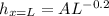
Definen that we need to find the average convection heat transfer coefficient in the entire plate lenght, so

`h=(1)/(L)\int\limit^L_0 h_x dx\\h=(1)/(L)\int\limit^L_0 AL^(-0.2)dx\\h=(A)/(0.8L)L^(0.8)\\h=1.25AL^(-0.2)`

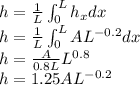
The ratio of the average heat transfer coefficient over the entire plate to the local convection heat transfer coefficient is

`R = (h)/(h_L)\\R= (1.25Al^(-0.2))/(AL^(-0.2))\\R= 1.25`