Answer:
Step-by-step explanation:
Moment of inertial of wheel I = M R²
Work done by force
= F d
It will be converted into rotational + linear kinetic energy
= 1/2 I ω² + 1/2 M V²
= 1/2 M R²ω² + 1/2 MV²
=1/2 MV²+1/2 MV²
MV²
MV² = Fd
V =
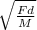
b )
acceleration of wheel
V² = 0 + 2 a d
a = V²/ 2d
= Fd / (M x 2d)
= F / 2M
if f be the force of friction
F - f = M a
= M x F / 2M
F - f = F /2
f = F /2
Friction force = F/2