Question

A beetle with a mass of 15.0 g is initially at rest on the outer edge of a horizontal turntable that is also initially at rest. The turntable, which is free to rotate with no friction about an axis through its center, has a mass of 95.0 g and can be treated as a uniform disk. The beetle then starts to walk around the edge of the turntable, traveling at an angular velocity of 0.0700 rad/s clockwise with respect to the turntable.(a) With respect to you, motionless as you watch the beetle and turntable, what is the angular velocity of the beetle? Use a positive sign if the answer is clockwise, and a negative sign if the answer is counter-clockwise.? rad/s(b) What is the angular velocity of the turntable (with respect to you)? Use a positive sign if the answer is clockwise, and a negative sign if the answer is counter-clockwise.? rad/s(c) If a mark is placed on the turntable at the beetle's starting point, how long does it take the beetle to reach the mark again?

Answer 1

a) TO solve the problem we need to apply the conservation of angular momentum,

`mR^(2)\omega_b + I\omega_t=0,`

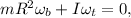
where,

I is the moment of inertia for the turntable, which is

m= the mass of the beetle

M= mass of the turntable

clearing
`\omega_t`,

`\omega_t=-(mR^2w_b)/(I)`

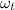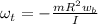
We know that
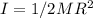`I= 1/2MR^2`. So,

Making a reference and asking where is the beetle we can see that it is on the turntale.

Therefore
`\omega = 0.0700 - 0.02210 = + 0.0579rad/s`

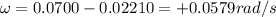
b) As we have seen in part a, it is
`-0.02210rad/s`

c) The angular velocity of the beetle is RELATIVE TO THE TURNTABLE, That is

`T=(2\pi)/(\omega)=(2\pi)/(0.7)= 89.76s`