Question

The most common source of copper (Cu) is the mineral chalcopyrite (CuFeS2). How many kilograms of chalcopyrite must be mined to obtain 305 g of pure Cu? Express your answer to three significant figures and include the appropriate units.

Answer 1

0.881 kilograms

Step-by-step explanation:

Mass of
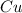`Cu` = 305 g

Molar mass of
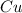`Cu` = 63.546 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

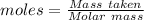
Thus,

`Moles= (305\ g)/(63.546\ g/mol)`

Moles of
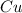`Cu` = 4.8 moles

Since in the formula of
`CuFeS_2`,

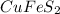1 mole of copper is present in 1 mole of
`CuFeS_2`

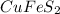
So,

4.8 mole of copper is present in 4.8 mole of
`CuFeS_2`

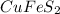
Moles of
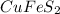`CuFeS_2` = 4.8 moles

Molar mass of
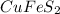`CuFeS_2` = 183.53 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

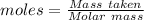
Thus,

`4.8\ moles= (Mass)/(183.53\ g/mol)`

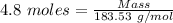
Moles of
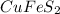`CuFeS_2` = 881 g

Also, 1 g = 0.001 kg

So,

0.881 kilograms of chalcopyrite must be mined to obtain 305 g of pure Cu.