Question

Match the following nonhomogeneous linear equations with the form of the particular solution yp for the method of undetermined coefficients.

? A B C D 1. y′′+y=t(1+sint)

? A B C D 2. y′′+4y=t2sin(2t)+(5t−7)cos(2t)

? A B C D 3. y′′+2y′+2y=3e−t+2e−tcost+4e−tt2sint

? A B C D 4. y′′−4y′+4y=2t2+4te2t+tsin(2t)


A. yp=t(A0t2+A1t+A2)sin(2t)+t(B0t2+B1t+B2)cos(2t)
B. yp=A0t2+A1t+A2+t2(B0t+B1)e2t+(C0t+C1)sin(2t)+(D0t+D1)cos(2t)
C. yp=Ae−t+t(B0t2+B1t+B2)e−tcost+t(C0t2+C1t+C2)e−tsint
D. yp=A0t+A1+t(B0t+B1)sint+t(C0t+C1)cost

Answer 1

1. D

2. A

3. C

4. B

Explanation:

1.

The particular function is:

`t(1 + sin(t)) = t + tsin(t)`

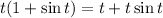
We have a first degree polynomial and a first degree polynomial multiplying a sine function.

The particular solution of a polynomial of degree n is another polynomial of degree n.

The particular solution of a sin(at) function is a sum of Asin(at) and Bcos(at).

So, the particular solution is

`A_(0)t + A_(1) + (B_(0) + B_(1))sin(t) + (C_(0)t + C_(1))cos(t)`

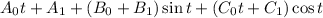
So 1 and D.

2.

The particular function is:

`t^(2)sin(2t)+(5t−7)cos(2t)`

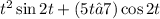
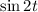`sin(2t)` and
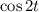`cos(2t)` have particular solutions in the same format. This means that we can multiply the particular solutions by t. The highest degree of the polynomials here is 2, so we have a sum of sin(2t) and cos(2t) each multiplied by a second order polynomial.

So

`yp=t(A_(0)t^(2)+A_(1)t+A2)sin(2t)+t(B_(0)t^(2)+B1t+B2)cos(2t)`

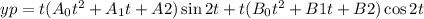
The particular solution of 2 is A.

3.

The particular function is

`3e^(−t)+2e{−t}cos(t)+4e{−t}t^(2)sin(t)`

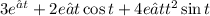
The particular solution of an exponential is another exponential.

So the solution is C.

4.

The particular function is:

`2t^(2) + 4te^(2t) + tsin(2t)`

Polynomial, polynomial multiplying an exponential and polynomial multiplying a sine functions.

So the answer is B.