Question

For a specific truck traveling at 50 miles per hour (mph), the distance x required to brake to a complete stop is normally distributed with a mean of 120 feet and a standard deviation of 12 feet. Suppose that this truck is traveling at a constant speed of 50 mph and a car abruptly moves into the path of the truck and stops at a distance of 150 feet from the truck. Assuming that the only way to avoid a collision is for the truck to brake to a complete stop, what is the probability that there will be a collision? Round your answer to 4 decimal places. Remember to round all z values to two decimal places.

Answer 1

There is a 0.62% probability that there will be a collision.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X. Subtracting 1 by the pvalue, we This p-value is the probability that the value of the measure is greater than X.

In this problem, we have that:

For a specific truck traveling at 50 miles per hour (mph), the distance x required to brake to a complete stop is normally distributed with a mean of 120 feet and a standard deviation of 12 feet. This means that
`\mu = 120, \sigma = 12`.

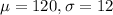Suppose that this truck is traveling at a constant speed of 50 mph and a car abruptly moves into the path of the truck and stops at a distance of 150 feet from the truck. Assuming that the only way to avoid a collision is for the truck to brake to a complete stop, what is the probability that there will be a collision?

There is going to be a collision if the car takes more than 150 feet to brake. So the probability of a collision is 1 subtracted by the pvalue of
`X = 150`.

`Z = (X - \mu)/(\sigma)`

`Z = (150 - 120)/(12)`

`Z = 2.5`

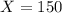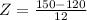
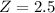
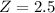`Z = 2.5` has a pvalue of 0.9938.

This means that there is a 1-0.9938 = 0.0062 = 0.62% probability that there will be a collision.