Question

Refrigerant-134a enters the compressor of a refrigeration system as saturated vapor at 0.14 MPa and leaves as superheated vapor at 0.8 MPa and 60°C at a rate of 0.054 kg/s. Determine the rates of energy transfers by mass into and out of the compressor. Assume the kinetic and potential energies to be negligible. The enthalpies of refrigerant-134a at the inlet and the exit are 239.19 kJ/kg and 296.82 kJ/kg, respectively.

Answer 1

16.02kW and 12.91kW

Step-by-step explanation:

Knowing the enthalpy data, we have to

`h1=239.16kJ/kg\\h2=296.81kJ/kg`

So,

`E_(mass,in)=mh_1`

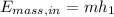
Here,

m=mass flow rate

h= Enthalpy of refrigerant at the compressor

Replacing

`E_(mass,in)=(0.054Kg/s)(239.16kJ/kg)\\E_(mass,in)=12.91kW`

The rate of energy transfer by mass into the compressor is 12.91kW

In the other hand we have,

`E_(mass,out)=mh_2`

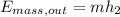
Replacing

`E_(mass,out)=(0.054Kg/s)(296.81kJ/kg)\\E_(mass,out)=16.02kW`

The rate of energy transfer by mass out of the compressor is 16.02 kW