Answer:
required time is 5.7 seconds
Step-by-step explanation:
solution
we first find here biot number by given formula that is
Bi =
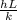
put here h is coefficient = 5000 and k = 50 W/m K and L is radius =
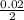 = 0.01
= 0.01
so
Bi =

Bi = 1
so for obtaining coefficient by table from term approx for the sphere at biot no 1
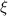 = 1.5708 and
= 1.5708 and
C = 1.2732
so
and
center line temp. is here
θ* =
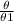
θ* =
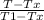
here T is 1000 K and Tx = 1300 K and T1 = 300 K
so
θ* =
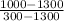
θ* = 0.3
so
radius for steel ball bearing ratio is here
r* =
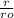
here r is 10 -1 and ro is 10
so
r* =
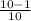
r* = 0.9
so that
fourier no for term approx for sphere is here
Fo =
![(-1)/(\xi^2) ln[ (\theta*)/(C) (1)/(\xi * r) sin ( \xi * r)]](https://img.qammunity.org/2020/formulas/engineering/college/wuv6a288g7xa2ih7mmboirflukot8u46js.png) ......1
......1
put here value
Fo =
![(-1)/(1.5708^2) ln[ (0.3)/(1.2732) (1)/(1.5708*0.9) sin (1.5708*0.9 *(180)/(\pi))]](https://img.qammunity.org/2020/formulas/engineering/college/jimsot9ec37sk5jwiwtpvtz0t1j8hcr3ao.png)
Fo = - 0.4053 ln ( 0.16462)
Fo = 0.7312
so time fpr 1 mm to 20 mm dia
Fo =

Fo =
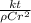
0.7312 =
![\frac{50 * t}{7800 * 500*10^(-3) ^2]()
t = 5.703 sec
so required time is 5.7 seconds