Answer with explanation:
As per given , we have
n= 88
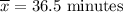
Population standard deviation :
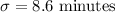
Critical value for 98% confidence interval :
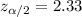 n
n
Margin of error :
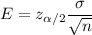
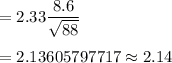
98% confidence interval :

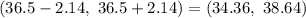
The 98% confidence interval (34.36, 38.64) found by normal distribution with the appropriate calculations for a standard deviation that is known is narrower than the interval (28.7,44.3) found by the t-distribution (population standard deviation is unknown) .