Question

Refrigerant-134a enters a 28-cm-diameter pipe steadily at 200 kPa and 20°C with a velocity of 5 m/s. The refrigerant gains heat as it flows and leaves the pipe at 180 kPa and 40°C. Determine (a) the volume flow rate of the refrigerant at the inlet, (b) the mass flow rate of the refrigerant, and (c) the velocity and volume flow rate at the exit.

Answer 1

V = 0.30787 m³/s

m = 2.6963 kg/s

v2 = 0.3705 m³/s

v2 = 6.017 m/s

Step-by-step explanation:

given data

diameter = 28 cm

steadily =200 kPa

temperature = 20°C

velocity = 5 m/s

solution

we know mass flow rate is

m = ρ A v

floe rate V = Av

m = ρ V

flow rate = V =
`(m)/(\rho)`

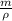
V = Av =
`(\pi)/(4) * d^2 * v1`

V =
`(\pi)/(4) * 0.28^2 * 5`

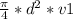
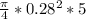
V = 0.30787 m³/s

and

mass flow rate of the refrigerant is

m = ρ A v

m = ρ V

m =
`(V)/(v)` =
`(0.30787)/(0.11418)`

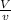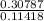
m = 2.6963 kg/s

and

velocity and volume flow rate at exit

velocity = mass × v

v2 = 2.6963 × 0.13741 = 0.3705 m³/s

and

v2 = A2×v2

v2 =
`(v2)/(A2)`

v2 =
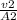
`(0.3705)/((\pi)/(4) * 0.28^2)`

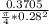
v2 = 6.017 m/s