Answer:
The temperature of the part won’t reach or exceed 141℉
Explanation:
Substituting the value of T= 141 the given equation becomes
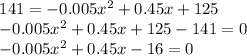
we know that discriminant D =
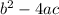
Three conditions: - D < 0: imaginary roots, D = 0: real and equal roots,
D > 0: two real and unequal roots Substituting a = -0.005, b = 0.045 and c = -16,
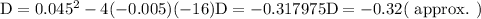 Therefore, it won't reach the temperature.
Therefore, it won't reach the temperature.