Question

Solving AequalsPeSuperscript rt for​ P, we obtain PequalsAeSuperscript negative rt which is the present value of the amount A due in t years if money earns interest at an annual nominal rate r compounded continuously. For the function Pequals4​,000eSuperscript negative 0.08 t​, in how many years will the ​$4​,000 be due in order for its present value to be ​$2​,000? In nothing ​years, the ​$4​,000 will be due in order for its present value to be ​$2​,000.

Answer 1

in 8.6 year will be $4000 be due in order present value $2000

Explanation:

given data

P = 4​,000
`e^(-0.08t)`

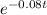
amount = $4000

present value = $2000

solution

we consider here present value P and amount A t time at annual nominal year rate r

so

P = A
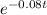`e^(-0.08t)` .................1

so put here P is $2000 and is and A is $4000

2000 = 4000
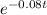`e^(-0.08t)` take ln both side

ln
`(2000)/(4000)` = ln
`e^(-0.08t)`

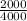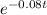
ln2 - ln 4 = -0.08 t

t = 8.664

so in 8.6 year will be $4000 be due in order present value $2000