Question

Water is pouring into an inverted cone at the rate of 3.14 cubic meters per minute. The height of the cone is 10 meters and the radius of its base is 5 meters. How fast is the water level rising when the water stands 7.5 meters in the cone?

Answer 1

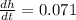`(dh)/(dt)=0.071` m/min

Step-by-step explanation:

You have to use the volume of a cone, which is:

`V=(1)/(3)\pi r^(2)h`

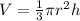
where r is the radius of the base and h is the height.

In this case, r=5 and h=10. The radius can be written as r=h/2

Replacing it in the equation:

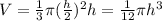`V=(1)/(3)\pi ((h)/(2))^(2) h=(1)/(12)\pi h^(3)` (I)

The rate of the volume is the derivate of volume respect time, therefore you have to perform the implicit differentiation of the previous equation and equal the result to 3.14 m³/min

`(dV)/(dt)=(\pi )/(12)(3)h^(2)(dh)/(dt) =(\pi )/(4)h^(2)(dh)/(dt)`

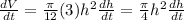
Replacing dV/dt= 3.14, h=7.5 and solving for dh/dt, which represents how fast the level is rising:

`3.14=(\pi )/(4)(7.5)^(2)(dh)/(dt)\\3.14=(225\pi )/(16)(dh)/(dt)`

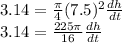
Multiplying by 16/225π both sides:

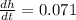`(dh)/(dt)=0.071` m/min