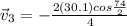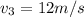Question

A(n) 18 kg object, initially at rest in free space, "explodes" into three segments. The masses of two of these segments are both 7 kg and their velocities are 4.3 m/s. The angle between the direction of motion of these segments is 74 ◦ . What is the speed of the third segment?

Answer 1

`v_3 = 12 m/s`

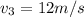
Step-by-step explanation:

As we know that during explosion of the object there is no external force on the system

So total momentum of the system will always remain conserved

so we will have

`m_1 v_1 + m_2v_2 + m_3 v_3 = 0`

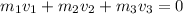
so here we can say

`\vec v_3 = - ((m_2 \vec v_2 + m_1 \vec v_1))/(m_3)`

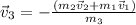
so here we know that

`m_1v_1 = m_2 v_2 = (7 )(4.3)`

`m_1v_1 = 30.1 kg m/s`

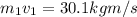
now we know that

`\vec v_3 = - (2mv cos(\theta)/(2))/(m_3)`

`\vec v_3 = - (2(30.1)cos(74)/(2))/(4)`

`v_3 = 12 m/s`