Answer: 0.2643
Explanation:
Let p be the population proportion and
 be the sample proportion .
be the sample proportion .
As per given question , we have
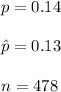
z-score :
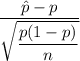

The required probability ( using z-table ):-
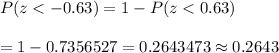
Hence, the probability that the proportion of books checked out in a sample of 478 books would be less than 13% = 0.2643