Question

The back of Monique’s property is a creek. Monique would like to enclose a rectangular area, using the creek as one side and fencing for the other three sides, to create a corral. If there is 180 feet of fence available, what is the maximum possible area of the corral?

Answer 1

4050 sq. feet.

Explanation:

Fencing is done on three sides of the rectangular area.

Given that there are 180 feet of fence available.

Then 2L + W = 180 ........(1), where L = length and W = width, of the rectangular plot.

Now, the area of the plot is given by A = LW

Now, from equation (1), we ger A = L (180 - 2L) ..... (2)

Then differentiating with respect to L in the both sides we get,

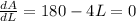`(dA)/(dL) = 180 - 4L =0` {Since condition for Area to be maximum is
`(dA)/(dL)=0`}

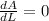⇒ L = 45 feet.

Now, from equation (2), we have
`A_(max) =L(180-2L) = 45(180 - 90) =4050` square feet.