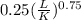Question

The firm's Cobb-Douglas production function is given as: Q (L comma K )equals L to the power of 0.75 end exponent K to the power of 0.25 end exponent Based on this information, the marginal product of capital (MPK) is:________

Answer 1

The marginal product of capital (MPK) is
`0.25((L)/(K))^(0.75)`

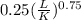
Explanation:

Data provided in the question:

The firm's Cobb-Douglas production function is given as

⇒ Q =
`L^(0.75)K^(0.25)`

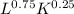
Now,

To find the marginal product of capital (MPK) computing the partial derivation of the Cobb-Douglas production function

i.e

`(\partial Q)/(\partial K) =(\partial (L^(0.75)K^(0.25)))/(\partial K)`

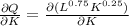
here, term L will be constant as it is a partial derivation with respect to K

thus,

`(\partial Q)/(\partial K) =0.25L^(0.75)K^(0.25-1)`

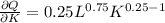
or

`(\partial Q)/(\partial K) =0.25L^(0.75)K^(-0.75)`

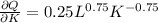
or

`(\partial Q)/(\partial K) =0.25((L)/(K))^(0.75)`

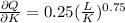
Hence,

the marginal product of capital (MPK) is
`0.25((L)/(K))^(0.75)`