Question

The small ball of mass m = 0.5 kg is attached to point A via string and is moving at constant speed in a horizontal circle of radius R = 0.16 m. The rate of rotation of the ball around the circle is ω = 2 rad/s. If the gravitational acceleration constant g is 10 m/s2 , find the value of height d.

Answer 1

d = 2.45 meters

Step-by-step explanation:

Mass of the ball, m = 0.5 kg

Radius of the circle, r = 0.16 m

The angular speed of the ball around the circle is,
`\omega=2\ rad/s`

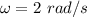
The attached figure shows the whole scenario. Let
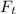`F_t` is the force acting on the ball in tangential direction. The forces will balanced each other at equilibrium.

In horizontal direction,

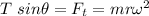`T\ sin\theta=F_t=mr\omega^2`................(1)

In vertical direction,

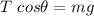`T\ cos\theta=mg`...............(2)

From equation (1) and (2) :

`tan\theta=(r\omega^2)/(g)`

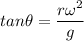
Also,

`tan\theta=(r)/(d)`

`d=(g)/(\omega^2)</p><p>`
`d=(9.8)/(2^2)`

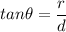
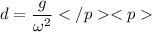
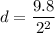
d = 2.45 meters

So, the value of d is 2.45 meters. Hence, this is the required solution.