Answer:
Explanation:
The Strong Induction Principle establishes that if a a subset S of the positive integers satisfies:
- S is a non-empty set.
- If m+1, m+2, ..., m+k ∈ S then m+k+1 ∈ S.
Then, we have that n ∈ S for all n ≥ k.
- Base case: Now, in our problem let S be the set of positive numbers than can be written as a sum of distinct powers of 2. Note that S is non-empty because, for example, 1, 2, 3 and 4 belongs to S:
 This is the so called base case, and in the definition above we set k = 1.
This is the so called base case, and in the definition above we set k = 1. - Inductive step: Now suppose that 1, 2, 3, .., k ∈ S. This is the inductive hypothesis. We are going to show that k+1 ∈ S. By hypothesis, since k ∈ S, it can be written as a sum of distinct powers of two, namely,
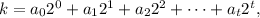 where
where
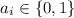 , i.e., every power of 2 occurs only once or not appear. Using the hint, we consider two cases:
, i.e., every power of 2 occurs only once or not appear. Using the hint, we consider two cases:
- k+1 is odd: In this case, k must be even. Note that
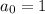 . If not were the case, then
. If not were the case, then
 and we can factor 2 in the representation of k:
and we can factor 2 in the representation of k:
 This will lead us to the contradiction that k is even. Then, adding 1 to k we obtain:
This will lead us to the contradiction that k is even. Then, adding 1 to k we obtain:
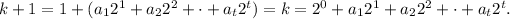
- k+1 is even: Then
 is an integer and is smaller than k, which means by the inductive hypothesis that belongs to S, that is,
is an integer and is smaller than k, which means by the inductive hypothesis that belongs to S, that is,
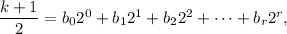 where
where
 , for all
, for all
 . Therefore, multiplying both sides by 2, we obtain
. Therefore, multiplying both sides by 2, we obtain
 This is a sum of distinct powers of 2, which implies that k+1 ∈ S.
This is a sum of distinct powers of 2, which implies that k+1 ∈ S.
Then we can conclude that n ∈ S , for all n ≥ 1, that is, every positive integer n can be written as a sum of distinct powers of 2.