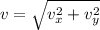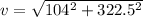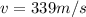Question

A plane drops a hamper of medical supplies from a height of 5300 m during a practice run over the ocean. The plane is horizontal velocity was 104 m/s at the instant the hamper was dropped. What is the magnitude of the overall velocity of the hamper at the instant it strikes the surface of the ocean

Answer 1

`v = 339 m/s`

Step-by-step explanation:

As we know that the horizontal speed of the plane is always constant

so here the speed in x direction always remain the same and given as

`v_x = 104 m/s`

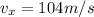
now in order to find vertical speed we can use kinematics so we will have

`v_f^2 - v_i^2 = 2a d`

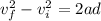
here we have

`v_f^2 - 0^2 = 2(9.81)(5300)`

`v_y = 322.5 m/s`

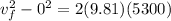
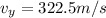
now net speed at which it will strike is given as

`v = √(v_x^2 + v_y^2)`

`v = √(104^2 + 322.5^2)`

`v = 339 m/s`