Answer:
IS NOT; ARE NOT
Explanation:
Given:
![\[ \begin{bmatrix} (1)/(4) & (1)/(4)\\ \\-1 & (-1)/(2) \end{bmatrix}\]](https://img.qammunity.org/2020/formulas/mathematics/high-school/w1qujo1vz86di32v0j5lztvmc678xx3uqj.png)
and
![\[A = \begin{bmatrix} (1)/(4) & (1)/(4) \\\\ -1 & (-1)/(2) \end{bmatrix}\]](https://img.qammunity.org/2020/formulas/mathematics/high-school/tgr5t7u8okv56jdf69er3f21febifcm6wr.png)
We say two matrices
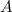 and
and
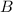 are inverses of each other when
are inverses of each other when
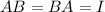 where
where
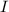 is the identity matrix.
is the identity matrix.
![\[I = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\]](https://img.qammunity.org/2020/formulas/mathematics/high-school/pbu3brzi7o5s1qd33hqsiairmbjjwt77l0.png)
So, for
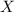 and
and
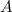 to be inverses of each other, we should have
to be inverses of each other, we should have
 .
.
Let us calculate
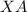 .
.
![\[\begin{bmatrix} -2 & -1 \\ 8 & 2 \end{bmatrix}\]](https://img.qammunity.org/2020/formulas/mathematics/high-school/6r656sefeyvb0wnrn7yhuoi84n4tp8rb02.png)
![\[\begin{bmatrix} (1)/(4) & (1)/(4) \\\\ -1 & (-1)/(2)\end{bmatrix}\]](https://img.qammunity.org/2020/formulas/mathematics/high-school/mvl3fjkna0gp24wo87lx4gujddgix0n4cn.png)

![\[\begin{bmatrix}(1)/(2) & 0 \\0 & 0 \end{bmatrix}\]](https://img.qammunity.org/2020/formulas/mathematics/high-school/qckasi10au9rzvzzqersh3f72kay8kxm9l.png)
This is clearly not equal to the identity matrix. So we conclude that the matrices are not inverses of each other.