Question

The on-line access computer service industry is growing at an extraordinary rate. Current estimates suggest that only 20% of the home-based computers have access to on-line services. This number is expected to grow quickly over the next five years. Suppose 25 people with home-based computers were randomly and independently sampled. Find the probability that more than 20 of those sampled currently do not have access to on-line services.

Answer 1

The probability is 0.4207

Explanation:

The probability of a home-based computer having access to on-line services is p = 0.2 (data from the exercise)

Then, the probability of a home-based computer not having access to on-line services is p = 1 - 0.2 = 0.8

We are going to use this probability (p = 0.8) to solve the exercise.

Let's define the random variable X

X : ''Number of home-based computers not having access to on-line services''

X can be modeled as a binomial random variable

X ~ Bi(p,n)

X ~Bi(0.8,25)

Where p is the success probability and n is the number of Bernoulli independent experiments we are taking place.

We are going to count ''a success'' as a computer not having access to on-line services.

The binomial probability function is :

`P(X=x)=(nCx)p^(x)(1-p)^(n-x)`

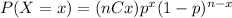
Where P(X=x) is the probability of the random variable X to assume the value x

nCx is the combinatorial number define as

`nCx=(n!)/(x!(n-x)!)`

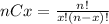
p is the success probability and n the number of Bernoulli independent experiments taking place.

In our exercise,

`p=0.8\\n=25`

We are looking for :

`P(X>20)=P(X=21)+P(X=22)+P(X=23)+P(X=24)+P(X=25)`

`P(X>20)=(25C21)0.8^(21)0.2^(4)+(25C22)0.8^(22)0.2^(3)+(25C23)0.8^(23)0.2^(2)+(25C24)0.8^(24)0.2^(1)+(25C25)0.8^(25)0.2^(0)`

`P(X>20)=0.1867+0.1358+0.0708+0.0236+0.8^(25)`

`P(X>20)=0.4207`

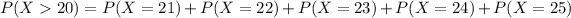
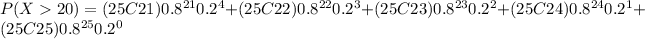
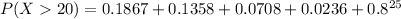
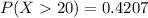
Finally, the probability of finding that more than 20 of 25 home-based computers do not have access to on-line services is 0.4207