Question

Three return steam lines in a chemical processing plan enter a collection tank operating at a steady state at 1 bar. Steam enters inlet 1 with flow rate of 0.8 kg/s and a quality of 0.9. Steam enters inlet 2 with flow rate of 2kg/s at 200 degrees C. Steam enters inlet 3 with flow rate 1.2 kg/s at 95 degrees C. Steam exits the tank at 1 bar. The rate of heat transfer from the collection tank is 40 kW. Neglecting kinetic and potential energy effects, determine for the steam exiting the tank:(a)Mass flow rate in kg/s (b) the temperature in degrees C.

Answer 1

a. 4kg/s

b. 99.97 °C

Step-by-step explanation:

Hello,

a. The resulting mass balance turns out into:

`F_1+F_2+F_3=F_(out)\\F_(out)=0.8kg/s+2kg/s+1.2kg/s=4kg/s`

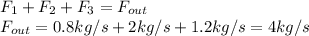
b. Now, the energy balance is:

`F_1h_1+F_2h_2+F_3h_3-Q_(out)=F_(out)h_(out)`

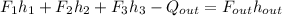
In such a way, the first enthalpy is taken as a liquid-vapor mixture at 1 bar and 0.9 quality, it means:

`h_1=hf(1bar)+xhfg(1bar)\\h_1=419.06kJ/kg+0.9*2256.5kJ/kg=2449.91kJ/kg`

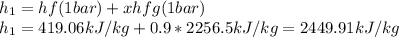
Second enthalpy is taken by identifying that stream as an overheated vapor at 1 bar and 200 °C, thus, the resulting enthalpy is:

`h_2=2875.5kJ/kg`

Then, the third enthalpy is taken by considering that at 95°C and 1 bar the water is a saturated liquid, thus:

`h_3=hf(95^0C)=398.09kJ/kg`.

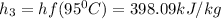Now, by solving for
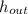`h_(out)`, we've got:

`h_(out)=(0.8kg/s*2449.91kJ/kg+2kg/s*2875.5kJ/kg+1.2kg/s*398.09kJ/kg-40kW)/(4kg/s) \\h_(out)=(8148.612kJ/s)/(4kg/s) \\h_(out)=2037.153kJ/kg`

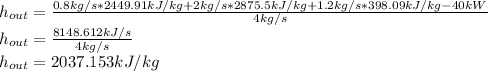
Finally, by searching for that value of enthalpy, one sees that at 1 bar, the exiting stream is a liquid-vapor mixture that is at 99.97 °C and has a 72%- quality.

(NOTE: all the data was extracted from Cengel's book 7th edition).

Best regards.