The polynomial 9x^5+36x^4+189x^3 in factored form is

Solution:
Given, polynomial equation is
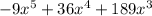
We have to find the factored form of the above given polynomial equation.
Let us solve it by grouping.
Now, take the polynomial ⇒
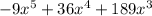
By taking common term out, we get
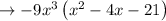
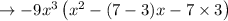
Grouping the terms we get,
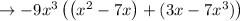
Taking common terms out from each group,
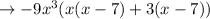

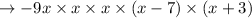
Thus the factored form of polynomial is found out