Question

The expression log (x^6y^3/z^9) can be written in the form Alog(x)+Blog(y)+Clog(z) where

A=
B=
C=

Answer 1

b

Explanation:

Answer 2

A = 6

B = 3

C = 9

Explanation:

We start by using repeatedly the product rule of logarithms that converts the logarithm of a product of two factors into the addition of logarithms:
`log (A*B)=log(A) + log(B)`:

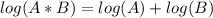`log (x^6*y^3*z^9)= log (x^6*[y^3*z^9])=log(x^6)+log(y^3*z^9)=\\=log(x^6)+log(y^3)+log(z^9)`

At this point we use on each term of the expression we found above, the power rule of logarithms that states:
`log(A^m)=m*log(A)`

This gives as:

`log(x^6)+log(y^3)+log(z^9)=6*log(x)+3*log(y)+9*log(z)`

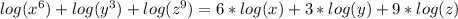
Therefore, the coefficients A, B, and C requested are:

A = 6

B = 3

C = 9