Question

A) Find the gravitational field strength of an asteroid with the mass of 3.2 * 10^3 kg and an average radius of 30 km when at a distance of 3 km from its surface

b) if an astronaut popped out of a worm hole (at rest) at 3 km from the asteroid
i) how long would it take him to fall to the asteroid’s surface?
ii) how fast would he be traveling when he hit it? (Assume acceleration stays constant)
iii) if a year is 3.16 * 10^7 s, how many years would it take for the astronaut to reach the asteroid?
Please show work, thanks

Answer 1

a)
`1.96\cdot 10^(-16) m/s^2`

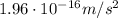
The gravitational field strength near the surface of the asteroid is given by:

`g=(GM)/((R+h)^2)`

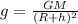
where

G is the gravitational constant

M is the mass of the asteroid

R the radius of the asteroid

h is the distance from the surface

Substituting the data of the asteroid:

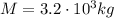`M=3.2\cdot 10^3 kg` is the mass

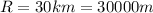`R=30 km = 30000 m` is the radius of the asteroid

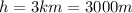`h=3 km = 3000 m` is the distance from the surface

We find

`g=((6.67\cdot 10^(-11))(3.2\cdot 10^3))/((30000+3000)^2)=1.96\cdot 10^(-16) m/s^2`

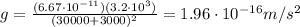
b) i)
`5.53\cdot 10^9 s`

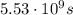
The acceleration of the astronaut popped out at 3 km from the surface is exactly that calculated at part a):

`g=1.96\cdot 10^(-16) m/s^2`

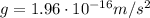
So, since its motion is at constant acceleration, we can find the time he takes to reach the surface using suvat equations:

`s=ut+(1)/(2)gt^2`

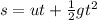
where

s = 3 km = 3000 m is his displacement to reach the surface

u = 0 is his initial velocity

t is the time

Solving for t,

`t=\sqrt{(2s)/(g)}=\sqrt{(2(3000))/(1.96\cdot 10^(-16) m/s^2)}=5.53\cdot 10^9 s`

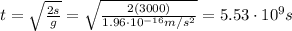
b) ii)
`1.08\cdot 10^(-6) m/s`

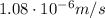
Again, we can use another suvat equation:

`v=u+gt`

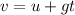
where

v is the final velocity

u is the initial velocity

g is the acceleration of gravity

t is the time

Since we have

u = 0

`t=5.53\cdot 10^9 s`

`g=1.96\cdot 10^(-16) m/s^2`

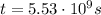
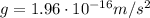
The velocity of the astronaut at the surface will be

`v=0+(1.96\cdot 10^(-16) m/s^2)(5.53\cdot 10^9)=1.08\cdot 10^(-6) m/s`

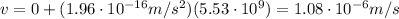
b) iii) 175 years

The duration of one year here is

`T=3.16\cdot 10^7 s`

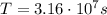
And the time it takes for the astronaut to reach the surface of the asteroid is

`t=5.53\cdot 10^9 s`

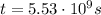
Therefore, to find the number of years, we just need to divide the total time by the duration of one year:

`n=(t)/(T)=(5.53\cdot 10^9 s)/(3.16\cdot 10^7)=175`

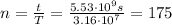
So, the astronaut will take 175 years to reach the surface.