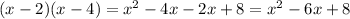Question

Binomial Multiplication (FOIL) paper (x-2)(x-4)

Answer 1

`x^(2)-6x+8`

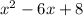
Explanation:

Given:

Binomial is
`(x-2)(x-4)`.

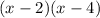In FOIL method, we first multiply the first term of each binomial. First terms are
`x` and
`x`.

⇒
`x* x=x^(2)`

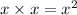
Next, we multiply the outer terms. Outer terms are
`x` and -4.

⇒
`x* -4=-4x`

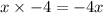
Next, we multiply the inner terms. Inner terms are -2 and
`x`.

`-2* x=-2x`

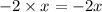
Lastly, we multiply the last terms of each binomial. Last terms are -2 and -4.

`-2* -4=8`

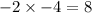
Now, we add all the results to get the answer.

Therefore,
`(x-2)(x-4)=x^(2)-4x-2x+8=x^(2)-6x+8`