Answer:
Length of the side AC =
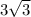 units
units
Explanation:
The given triangle ABC is a right triangle.
Here, AB = 6 units ( hypotenuse)
CB = 3 units (base)
Now, as the triangle is a right triangle, so by
PYTHAGORAS THEOREM
In a right triangle,
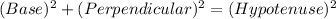
So, here in ΔABC:
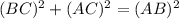
or,
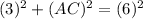
⇒
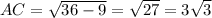
or, the length of the side AC =
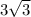 units
units