Question

Suppose that x and y vary inversely, and x = 10 when y = 8. Write the function that models the inverse variation.

a. y=2/x
b. y=18/x
c. y=80/x
d. y=0.8x

Answer 1

c.
`y=(80)/(x)`

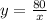
Explanation:

Given:

`x` and
`y` vary inversely.

Therefore, we can express y in terms of x as:

`y=(k)/(x)`

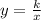
Where,
`k` is a constant of proportionality.

Now, at
`x=10,y=8`

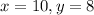
Plug in 10 for
`x` and 8 for
`y` in the above equation and solve for
`k`.

This gives,

`8=(k)/(10)\\k=8* 10=80`

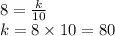
Therefore, the function that models the inverse variation is :

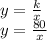`y=(k)/(x)\\y=(80)/(x)`.