Answer:
∠ R
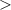 90°
90°
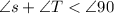
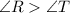

Explanation:
Given that in triangle RST
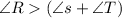
Now as per condition one angle is greater than sum of other two angles.
Since in triangle ,sum of all three angles = 180°
Hence if one angle is 90° then sum of other two must be equal to 90°
And if one angle is 90° then only other two angle be 45° each
Here Let if angle s = angle T = 30° then with this condition angle r is 120° , which is greater than 90°
So, from above it conclude that
For ,
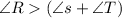
∵ ∠ R = 120° , then it is greater than 90°
I.e , ∠ R
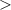 90°
90°
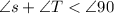
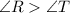
 Answer
Answer