Answer:
The equation of parabola is ( x - 4 )² = 4 ( y - 10)
Explanation:
Given as :
The end points latus rectum is ( 2 , 9 ) and ( 6 , 9 )
The equation of parabola is
( x - h )² = 4p ( y - k)
Where ( h , k ) is vertex
And 4p =
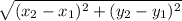
Or, 4p =
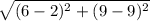
∴ p = 1
∵ focus is mid point of latus rectum
so ,
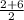 ,
,
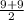
or focus = ( 4 , 9)
So, vertex (h , k) = ( 4 , 9-1 ) = ( 4 , 8 )
SO, equation is
( x - 4 )² = 4×1 ( y - 8)
Or, ( x - 4 )² = 4 ( y - 8 )
Hence The equation of parabola is ( x - 4 )² = 4 ( y - 8 ) Answer