Question

1. Determine whether -3 is a root of x3 + 3x2 + x + 1 = 0.

Explain.

2. Write a polynomial equation of least degree with
roots 3,-1, 2i, and -2i. How many times does the
graph of the related function intersect the x-axis?

Answer 1

1. The given equation does not have root at x = - 3.

2. (x - 3) (x + 1) (x² + 4) = 0

This curve will intersect twice the x-axis.

Explanation:

1. If the right hand side of the equation
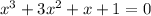`x^(3) +3x^(2) +x+1 =0` ......... (1) becomes same as the left hand side by putting x = - 3, then only we can conclude that x = - 3 is a root of the equation.

But in this case
`(-3)^(3) + 3(-3)^(2)+(-3) +1 \\eq  0`.

Therefore, x = - 3 is not a root of the above equation (1).

2. The equation of the polynomial with roots 3, -1, 2i, and -2i is

(x - 3) (x + 1) (x - 2i) (x + 2i) = 0

⇒ (x - 3) (x + 1) (x² + 4) = 0 (Answer)

Therefore, the graph of the above curve will intersect twice the x-axis in a real coordinate plane, at x = 3 and at x = -1. (Answer)